| Time Limit | $1$ 秒/Second(s) | Memory Limit | $512$ 兆字节/Megabyte(s) |
| 提交总数 | $1$ | 正确数量 | $1$ | "
| 裁判形式 | 标准裁判/Standard Judge | 我的状态 | 尚未尝试 |
| 难度 | 分类标签 | 动态规划 |
红黑树是一类特殊的二叉搜索树，其中每个结点被“染成”红色或黑色。若将二叉搜索树结点中的空指针看作是指向一个空结点，则称这类空结点为二叉搜索树的前端结点。并规定
所有前端结点的高度为-1。
一棵红黑树是满足下面“红黑性质”染色二叉搜索树：
(1)每个结点被染成红色或黑色；
(2)每个前端结点为黑色结点；
(3)任一红结点的儿子结点均为黑结点；
(4)在从任一结点到其子孙前端结点的所有路径上具有相同的黑结点数。
从红黑树中任一结点 x 出发(不包括结点 x)，到达一个前端结点的任意一条路径上的黑
结点个数称为结点 x 的黑高度，记作 bh(x)。红黑树的黑高度定义为其根结点的黑高度。
图示的二叉搜索树是一棵红黑树。标在结点旁边的数字是相应结点的黑高度。
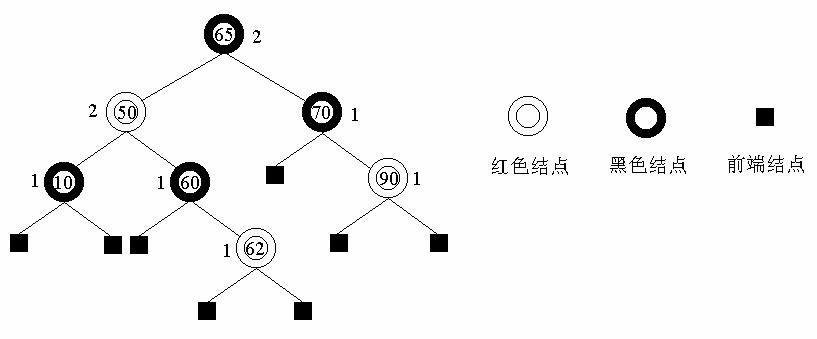
图 3-3 红黑树
«算法设计：
给定正整数 n，试设计一个算法，计算出在所有含有 n 个结点的红黑树中，红色内结点
个数的最小值和最大值。
8
1
4
| 本题记录 | 用 户（点击查看用户） | 运行号（点击购买题解） | 时 间 |
|---|---|---|---|
| 算法最快[$0 $ms] | 大喵-sama | 900297 | 2022-10-11 16:15:56 |
| 内存最少[$2020 $KB] | 大喵-sama | 900297 | 2022-10-11 16:15:56 |
| 第一AC | 大喵-sama | 900297 | 2022-10-11 16:15:56 |
| 第一挑战 | 大喵-sama | 900297 | 2022-10-11 16:15:56 |
| 竞赛编号 | 竞赛名称 | 竞赛时间 | 访问比赛 |
|---|