| Time Limit | $1$ 秒/Second(s) | Memory Limit | $512$ 兆字节/Megabyte(s) |
| 提交总数 | $0$ | 正确数量 | $0$ | "
| 裁判形式 | 标准裁判/Standard Judge | 我的状态 | 尚未尝试 |
| 难度 | 分类标签 | 回溯 |
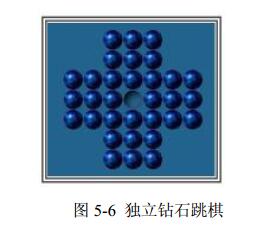
独立钻石跳棋的棋盘上有 33 个方格，每个方格中可放 1 枚棋子。棋盘中最多可摆放 32枚棋子。 下棋的规则是任一棋子可以沿水平或垂直方向跳过与其相邻的棋子进入空着的方格并吃掉被跳过的棋子。试设计一个算法，对于任意给定的棋盘布局，找出一种下棋方法，使得最终棋盘上只剩下一个棋子。
算法设计：
对于给定的独立钻石跳棋的棋盘初始布局，和棋盘上最终剩下的棋子所在的位置(x,y)，计算一种遵循下棋的规则下棋方法， 使最终棋盘上仅在位置(x,y)处有一枚棋子。当(x,y)=(0,0)时，表示不指定棋子的最终位置。棋子位置的坐标定义如下。
8
4 1
5 2
5 3
6 3
3 4
4 4
4 5
4 6
0 0
(3,4) (5,4)
(4,6) (4,4)
(4,4) (6,4)
(6,4) (6,2)
(6,2) (4,2)
(4,1) (4,3)
(5,3) (3,3)
| 本题记录 | 用 户（点击查看用户） | 运行号（点击购买题解） | 时 间 |
|---|---|---|---|
| 算法最快[$ $ms] | |||
| 内存最少[$ $KB] | |||
| 第一AC | |||
| 第一挑战 |
| 竞赛编号 | 竞赛名称 | 竞赛时间 | 访问比赛 |
|---|