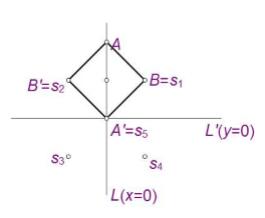
假设直线L和L'相交于原点O。假设S ={s1,s2,...,sn}是平面上的n个点。你打 算找四个点满足如下条件:
1. A ∈ L 而 A' ∈ L'。
2. B,B'都属于S;即 B∈S 且B'∈S。
3. A,A'的中点与B,B'的中点重叠。这意味着ABA'B'是一个平行四边形(或者退 化的平行四边形)。
4. 平行四边形ABA'B'的面积最大。
1535: 平行四边形
| Time Limit | $1$ 秒/Second(s) | Memory Limit | $512$ 兆字节/Megabyte(s) |
| 提交总数 | $3$ | 正确数量 | $1$ | "
| 裁判形式 | 标准裁判/Standard Judge | 我的状态 | 尚未尝试 |
| 难度 | 分类标签 |
Description
Input
只包含一组测试数据。
第一行有4个整数a, b, a', b',分别描述L和L'的坐标方程。具体来说,L的方程 为 ax + by = 0 ;而 L'的方程为 a'x + b'y = 0。
第二行有一个整数n。
接下来n行每行两个整数,表示一对坐标,描述S中的n个点。
保证n <= 106,其他输入整数的绝对值不超过104;保证ab'≠ba',a2+b2>0,a′2+b′2>0。
第一行有4个整数a, b, a', b',分别描述L和L'的坐标方程。具体来说,L的方程 为 ax + by = 0 ;而 L'的方程为 a'x + b'y = 0。
第二行有一个整数n。
接下来n行每行两个整数,表示一对坐标,描述S中的n个点。
保证n <= 106,其他输入整数的绝对值不超过104;保证ab'≠ba',a2+b2>0,a′2+b′2>0。
Output
输出一个整数,表示最大平行四边形的面积四舍五入到整数的值。
保证所有数据中,最大面积在四舍五入前的小数部分在[0,0.4] ⋃ [0.6,1)中。
保证所有数据中,最大面积在四舍五入前的小数部分在[0,0.4] ⋃ [0.6,1)中。
Sample Input复制
1 0 0 1
5
1 1
-1 1
-1 -1
1 -1
0 0
Sample Output复制
2
提示
Hint
推荐代码 查看1535 所有题解 上传题解视频得图灵币
| 本题记录 | 用 户(点击查看用户) | 运行号(点击购买题解) | 时 间 |
|---|---|---|---|
| 算法最快[$0 $ms] | AOJ大管家 | 435567 | 2019-05-31 00:09:36 |
| 内存最少[$2020 $KB] | AOJ大管家 | 435567 | 2019-05-31 00:09:36 |
| 第一AC | AOJ大管家 | 435567 | 2019-05-31 00:09:36 |
| 第一挑战 | 严庭竹@计算机科学与技术162 | 37468 | 2016-12-06 17:53:30 |
赛题来源/所属竞赛 2016年中国大学生程序设计竞赛 N/A
| 竞赛编号 | 竞赛名称 | 竞赛时间 | 访问比赛 |
|---|