稀疏矩阵的存储不宜用二维数组存储每个元素,那样的话会浪费很多的存储空间。所以可以使用一个一维数组存储其中的非零元素。这个一维数组的元素类型是一个三元组,由非零元素在该稀疏矩阵中的位置(行号和列号对)以及该元组的值构成。
矩阵转置就是将矩阵行和列上的元素对换。
现在就请你对一个稀疏矩阵进行转置。以下是稀疏矩阵转置的算法描述:
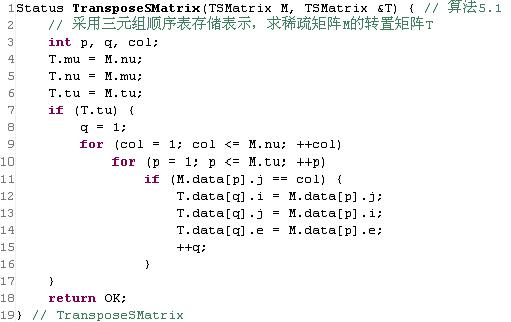
图:稀疏矩阵转置的算法描述
| Time Limit | $1$ 秒/Second(s) | Memory Limit | $512$ 兆字节/Megabyte(s) |
| 提交总数 | $16$ | 正确数量 | $11$ | "
| 裁判形式 | 标准裁判/Standard Judge | 我的状态 | 尚未尝试 |
| 难度 | 分类标签 |
稀疏矩阵的存储不宜用二维数组存储每个元素,那样的话会浪费很多的存储空间。所以可以使用一个一维数组存储其中的非零元素。这个一维数组的元素类型是一个三元组,由非零元素在该稀疏矩阵中的位置(行号和列号对)以及该元组的值构成。
矩阵转置就是将矩阵行和列上的元素对换。
现在就请你对一个稀疏矩阵进行转置。以下是稀疏矩阵转置的算法描述:

图:稀疏矩阵转置的算法描述
输入的第一行是两个整数r和c(r*c <= 12500),分别表示一个包含很多0的稀疏矩阵的行数和列数。接下来有r行,每行有c个整数,表示这个稀疏矩阵的各个元素。
输出c行,每行有r个整数,每个整数后跟一个空格。该结果为输入稀疏矩阵的转置矩阵。
6 7
0 12 9 0 0 0 0
0 0 0 0 0 0 0
-3 0 0 0 0 14 0
0 0 24 0 0 0 0
0 18 0 0 0 0 0
15 0 0 -7 0 0 0
0 0 -3 0 0 15
12 0 0 0 18 0
9 0 0 24 0 0
0 0 0 0 0 -7
0 0 0 0 0 0
0 0 14 0 0 0
0 0 0 0 0 0
提示:
我使用的严老师纸质书中用union类型来表示稀疏矩阵类型,这是有问题的,应该使用struct来表示该类型。
注意理解为什么转置算法中,以列从小到大来进行转置。实际上只需一个循环就能够完成转置而不需将列从小到大来处理,转置后的矩阵虽然是正确的但却乱掉了,以至于在各种处理中会增加复杂。(其实就本题而言,如果不以列从小到大处理将导致输出困难,输出的复杂度增加)
总结:
矩阵是一个应用很广泛的工具和课题。看看《黑客帝国》就知道了。现在初步给大家介绍矩阵的操作,以后有机会还会详细讨论矩阵的。
| 本题记录 | 用 户(点击查看用户) | 运行号(点击购买题解) | 时 间 |
|---|---|---|---|
| 算法最快[$0 $ms] | Qiqy | 581602 | 2020-05-03 11:16:33 |
| 内存最少[$972 $KB] | 范晋豪@信息与计算科学142 | 152698 | 2017-11-16 15:10:14 |
| 第一AC | 范晋豪@信息与计算科学142 | 152698 | 2017-11-16 15:10:14 |
| 第一挑战 | 范晋豪@信息与计算科学142 | 152698 | 2017-11-16 15:10:14 |
| 竞赛编号 | 竞赛名称 | 竞赛时间 | 访问比赛 |
|---|