Treap
A binary search tree can be unbalanced depending on features of data. For example, if we insert n elements into a binary search tree in ascending order, the tree become a list, leading to long search times. One of strategies is to randomly shuffle the elements to be inserted. However, we should consider to maintain the balanced binary tree where different operations can be performed one by one depending on requirement.
We can maintain the balanced binary search tree by assigning a priority randomly selected to each node and by ordering nodes based on the following properties. Here, we assume that all priorities are distinct and also that all keys are distinct.
binary-search-tree property. If v is a left child of u, then v.key<u.key and if v is a right child of u,then u.key<v.keyheap property.
heap property. If v is a child of u, then v.priority<u.priority
This combination of properties is why the tree is called Treap (tree + heap).
An example of Treap is shown in the following figure.
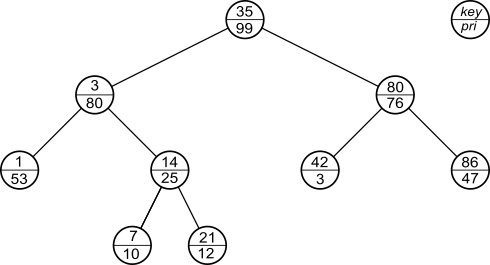
Insert
To insert a new element into a Treap, first of all, insert a node which a randomly selected priority value is assigned in the same way for ordinal binary search tree. For example, the following figure shows the Treap after a node with key = 6 and priority = 90 is inserted.
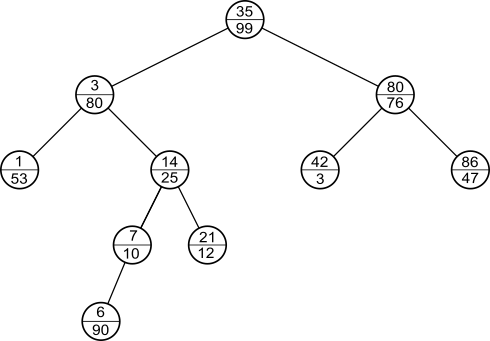
It is clear that this Treap violates the heap property, so we need to modify the structure of the tree by rotate operations. The rotate operation is to change parent-child relation while maintaing the binary-search-tree property.

The rotate operations can be implemented as follows.
rightRotate(Node t)
Node s = t.left
t.left = s.right
s.right = t
return s // the new root of subtree
leftRotate(Node t)
Node s = t.right
t.right = s.left
s.left = t
return s // the new root of subtree
The following figure shows processes of the rotate operations after the insert operation to maintain the properties.
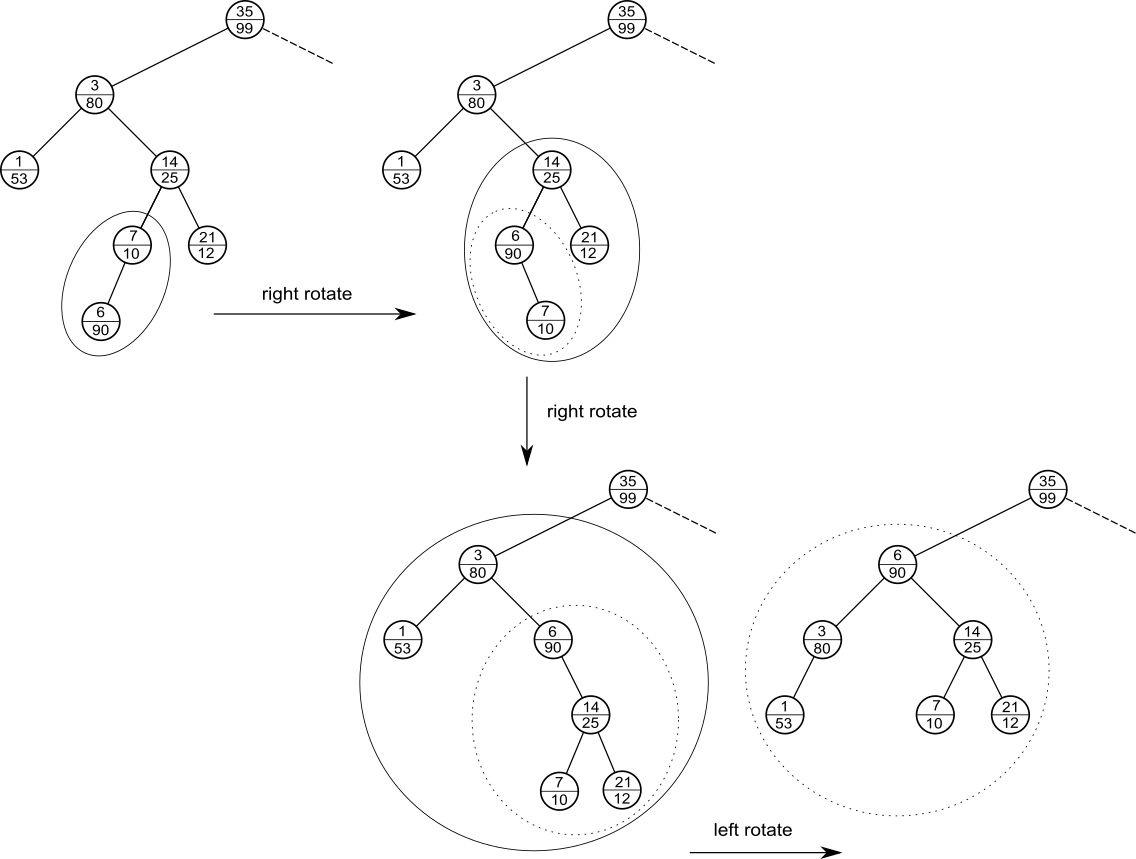
The insert operation with rotate operations can be implemented as follows.
insert(Node t, int key, int priority) // search the corresponding place recursively
if t == NIL
return Node(key, priority) // create a new node when you reach a leaf
if key == t.key
return t // ignore duplicated keys
if key < t.key // move to the left child
t.left = insert(t.left, key, priority) // update the pointer to the left child
if t.priority < t.left.priority // rotate right if the left child has higher priority
t = rightRotate(t)
else // move to the right child
t.right = insert(t.right, key, priority) // update the pointer to the right child
if t.priority < t.right.priority // rotate left if the right child has higher priority
t = leftRotate(t)
return t
Delete
To delete a node from the Treap, first of all, the target node should be moved until it becomes a leaf by rotate operations. Then, you can remove the node (the leaf). These processes can be implemented as follows.
delete(Node t, int key) // seach the target recursively
if t == NIL
return NIL
if key < t.key // search the target recursively
t.left = delete(t.left, key)
else if key > t.key
t.right = delete(t.right, key)
else
return _delete(t, key)
return t
_delete(Node t, int key) // if t is the target node
if t.left == NIL && t.right == NIL // if t is a leaf
return NIL
else if t.left == NIL // if t has only the right child, then perform left rotate
t = leftRotate(t)
else if t.right == NIL // if t has only the left child, then perform right rotate
t = rightRotate(t)
else // if t has both the left and right child
if t.left.priority > t.right.priority // pull up the child with higher priority
t = rightRotate(t)
else
t = leftRotate(t)
return delete(t, key)
Write a program which performs the following operations to a Treap T based on the above described algorithm.
insert (k, p): Insert a node containing k as key and p as priority to T.
find (k): Report whether T has a node containing k.
delete (k): Delete a node containing k.
print(): Print the keys of the binary search tree by inorder tree walk and preorder tree walk respectively.