Maximum Heap
A binary heap which satisfies max-heap property is called max-heap. In a max-heap, for every node ii other than the root, A[i]≤A[parent(i)], that is, the value of a node is at most the value of its parent. The largest element in a max-heap is stored at the root, and the subtree rooted at a node contains values no larger than that contained at the node itself.
Here is an example of a max-heap.
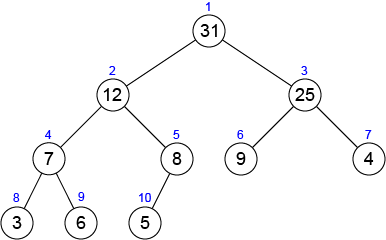
Write a program which reads an array and constructs a max-heap from the array based on the following pseudo code.
maxHeapify(A,i) move the value of A[i] down to leaves to make a sub-tree of node i a max-heap. Here, H is the size of the heap.
1 maxHeapify(A, i)
2 l = left(i)
3 r = right(i)
4 // select the node which has the maximum value
5 if l ≤ H and A[l] > A[i]
6 largest = l
7 else
8 largest = i
9 if r ≤ H and A[r] > A[largest]
10 largest = r
11
12 if largest ≠ i // value of children is larger than that of i
13 swap A[i] and A[largest]
14 maxHeapify(A, largest) // call recursively
The following procedure buildMaxHeap(A) makes AA a max-heap by performing maxHeapify in a bottom-up manner.
1 buildMaxHeap(A)
2 for i = H/2 downto 1
3 maxHeapify(A, i)