Optimal Binary Search Tree
Optimal Binary Search Tree is a binary search tree constructed from n keys and n+1 dummy keys so as to minimize the expected value of cost for a search operation.
We are given a sequence K=k1,k2,...,kn of n distinct keys in sorted order (k1<k2<...<kn),
and we wish to construct a binary search tree. For each key ki, we have a probability pi that a search will be for ki. Some searches may be for values not in K, and so we also have n+1 dummy keys d0,d1,d2,...,dn representing values not in K. The dummy keys di(0≤i≤n) are defined as follows:
if i=0, then di represents all values less than k1
if i=n, then di represents all values greater than kn
if 1≤i≤n−1, then di represents all values between ki and ki+1
For each dummy key di, we have a probability qi that a search will correspond to di. For pi(1≤i≤n) and qi(0≤i≤n), we have
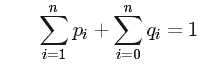
Then the expected cost of a search in a binary search tree T is

where depthT(v) is the depth of node v in T. For a given set of probabilities, our goal is to construct a binary search tree whose expected search cost is smallest. We call such a tree an optimal binary search tree.
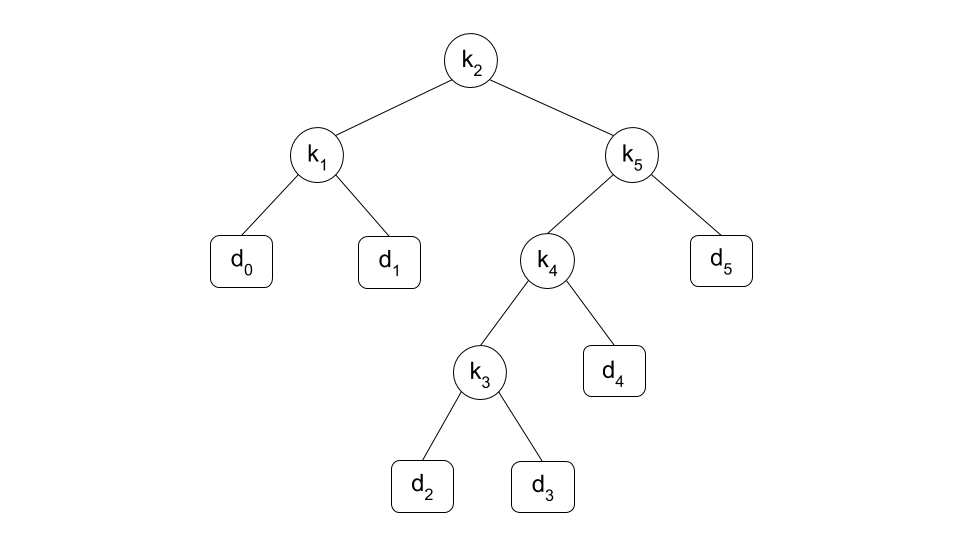
For example, the following figure shows the optimal binary search tree obtained from Sample Input 1.
Task
Write a program which calculates the expected value of a search operation on the optimal binary search tree obtained by given pi that a search will be for ki and qi that a search will correspond to di.
