Problem 2973 --Another Chess Problem

2973: Another Chess Problem

上一题 正确率: $100.00\%$ 下一题
"
Time Limit $1$ 秒/Second(s) Memory Limit $512$ 兆字节/Megabyte(s)
提交总数 $2$ 正确数量 $2$
裁判形式 标准裁判/Standard Judge 我的状态 尚未尝试
难度 分类标签

Description

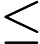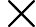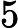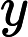
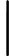
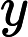
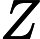
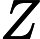
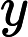
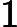
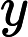
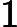
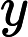
You are given an infinite set S={(x,y)|x,y∈Z,¬∃i,j∈Zs.t.x=2i+j,y=i−2j}and two pairs (x1,y1),(x2,y2)∈S. 

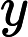
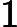
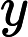
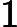
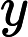
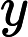
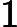
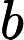
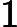
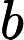
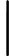
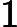
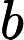
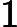
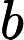
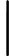You have a pair (x,y) in your right pocket which equals to (x1,y1) in the beginning. You can pay Y_UME a coin at a time and then change (x,y) to one element in S whose distance to (x,y) is 1. The distance between (a1,b1) and (a2,b2) is defined as |a1−a2|+|b1−b2|. 

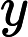
You expect to get (x2,y2) and minimize the number of coins given to Y_UME. Output the minimum number of coins and output the number of different ways to achieve the goal modulo 998244353. 

Note that two ways differ if and only if there exsits some i such that i-th steps in the two ways are different.

Input

The first line contains one positive integer T(T≤2×105) denoting the number of test cases.

Each case starts with a line containing four integers x1,y1,x2,y2(−105≤x1,y1,x2,y2≤105).

Output

For each test case, output one line containing two integers denoting the minimum number of coins and the number of different ways modulo 998244353.

Sample Input复制

3
1 1 5 2
1 1 2 5
1 1 1 1

Sample Output复制

7 5
5 1
0 1

推荐代码 查看2973 所有题解 上传题解视频得图灵币

本题记录 用 户（点击查看用户） 运行号（点击购买题解） 时 间
算法最快[$253 $ms] 刘成健 467511 2019-09-11 17:25:54
内存最少[$0 $KB] 淡意的温柔 605348 2020-07-03 15:12:24
第一AC 刘成健 467511 2019-09-11 17:25:54
第一挑战 刘成健 467511 2019-09-11 17:25:54

赛题来源/所属竞赛 2019 Multi-University Training Contest 2 N/A

竞赛编号 竞赛名称 竞赛时间 访问比赛