In the mathematical discipline of graph theory, the line graph of a simple undirected graph G is another simple undirected graph L(G) that represents the adjacency between every two edges in G.
Precisely speaking, for an undirected graph G without loops or multiple edges, its line graph L(G) is a graph such that
- each vertex of L(G) represents an edge of G; and
- two vertices of L(G) are adjacent if and only if their corresponding edges share a common endpoint in G.
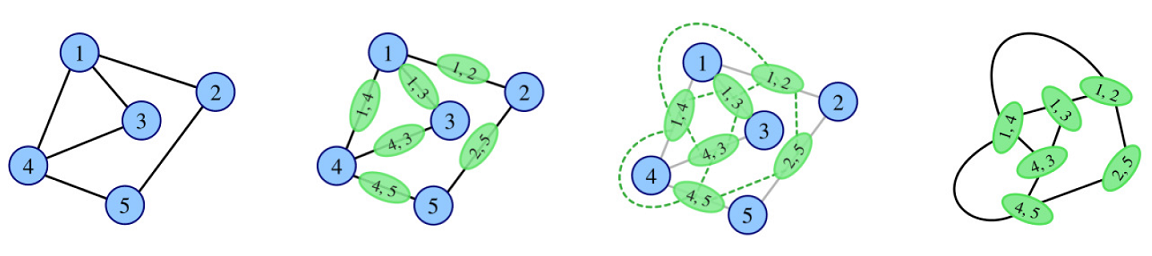
Given a simple undirected graph G, Rounddog's study aims to find the maximum cliques in its line graph L(G) and he decides to make some critical results of his early study as a challenge for you.
In this problem, you are given a simple undirected graph G and a small positive integer k. After finding all maximum cliques in Lk(G), where L0(G)=G and Ls(G)=L(Ls−1(G)) for each positive integer s, you need to show Rounddog the number of vertices in one of the maximum cliques and the number of distinct maximum cliques modulo 1000000007.
Here a subset of vertices of an undirected graph is called clique if and only if there is an edge between each pair of vertices in the subset, and maximum cliques are those cliques with the maximum number of vertices.