Problem 3507 --Coin Game

3507: Coin Game

上一题 正确率: $0.00\%$ 下一题
"
Time Limit $1$ 秒/Second(s) Memory Limit $512$ 兆字节/Megabyte(s)
提交总数 $0$ 正确数量 $0$
裁判形式 标准裁判/Standard Judge 我的状态 尚未尝试
难度 分类标签

Description

There are nmachines in front of you, and each of them has a cute button on it.
For the i-th machine, if you push the button on it, it will give you a coin valued at ai. If you push the button again, it will give you a coin valued at bi. If you push the button the third time, it will give you a coin valued at aiagain. However, it won't give you coins any more even you push the button because the i-th machine only has three coins.
Now you want to obtain kcoins from these machines, and you should make the total value of these coins as maximum as possible. Let's denote the maximum total value of these kcoins as f(k).
You are required to output the value of f(1)⊕f(2)⊕f(3)⊕⋯⊕f(m), where mis a given number and ⊕means the xor operatation.

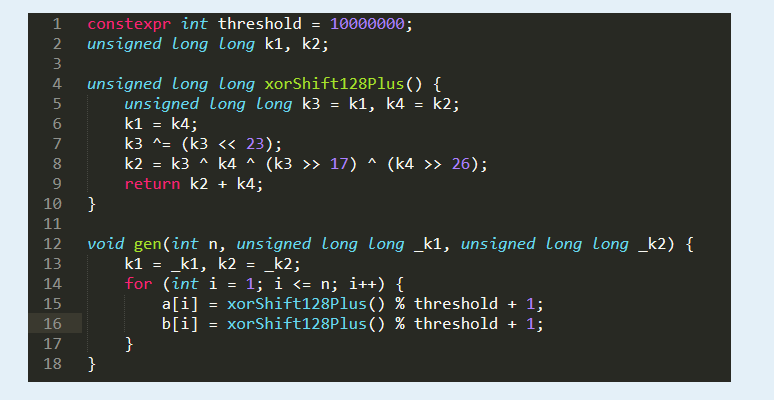
To avoid spending too much time reading all the data, we use xorshift128plus algorithm to generate the testdata, this algorithm is parameterized with two initial seed k1and k2. Please refer to the code (written in C++) in the below:


Input

There are multiple test cases,please read until the end of the file.
For each test case, it contains only four integer n,m,k1,k2. 1≤n≤5×106, 1≤m≤1.5×107, 1≤k1,k2≤1012in one line. 

Output

Output the answer in one line for each test case.

Sample Input复制

2 6 123456789 987654321
10 20 19260817 71806291

Sample Output复制

6935157
41506271

提示

In the first test case of the sample input, there are 2machines, and the first machine will give you the coins valued at (406905,1803337,406905)and (491922,4734236,491922).
f(1)=491922,f(2)=5226158,f(3)=5718080,f(4)=7436400,f(5)=7928322,f(6)=8335227

推荐代码 查看3507 所有题解 上传题解视频得图灵币

本题记录 用 户（点击查看用户） 运行号（点击购买题解） 时 间
算法最快[$ $ms]
内存最少[$ $KB]
第一AC
第一挑战

赛题来源/所属竞赛 2020 Multi-University Training Contest 10 N/A

竞赛编号 竞赛名称 竞赛时间 访问比赛
AOJ