"想要传达的，仅仅只有一件是将瞬间保存下来的永远。"
小 A 曾经是绘画的天才，他可以奇迹般地将他所见的一切通过绘画记录下来。但如今的他因为事故失去了用惯用手作画的能力。不过，好在是小 A 还没有放弃绘画，他尝试用自己曾经锻炼出来的技巧以及他的毅力再一次向绘画挑战。
具体的，小 A 定义一副画的价值为 f(l, r) (l ≤ r , 
)，表示在集合 S = {l, l + 1, ..., r} 中选取一些数，满足选出的数字的乘积为完全平方数的方案数。小 A 画出一副价值为 f(l, r) 的画，意味着小 A 把绘画中的每个元素与数字中的 {l, l + 1, ..., r} 一一对应。对于一个选取方案 U = {x0, ..., xk} (
) 满足 
为完全平方数，小 A 认为这对应了一种艺术审美视角，因此会使画的价值提升。注意：其中空集也算一种合法的选法。
曾经的小 A 可以控制参数 l, r ，但如今他失去了曾经的能力。不过好在他的身体替他记住了曾经的绘画技巧，于是他可以控制绘画的大体走向，但是小范围的细节仍然会有波动。也就是现在他所做出的画实际的价值为 f(l + x, r - y)。其中 x , y 是两个随机的参数。对于每一个正整数 i (1 ≤ i ≤ n)，x = i 的概率为 pi，y = i 的概率为 qi。
设 l' = l + x, r' = r - y, d = r' - l'， 小 A 想知道，对于所有的 d = r - l - 2n + 1, r - l - 2n + 2, ..., r - l - 1 ，其中画作的期望权值为多少。
答案对 998244353 取模后输出。
设答案的最简真分数形式可以表示成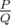 
，输出 P × Q - 1 ± od {998244353} 的结果。数据保证 Q 不为 998244353 的倍数。
)。
。
。