正向传播与反向传播是现代神经网络的基础, 小 M 在机器学习课程中成绩很不好, 想利用这次安徽省机器人大赛的机会实践一下机器学习的基础理论, 从零开始实现一个机器学习框架. 他手动定义了一个神经元间的结构, 定义了损失函数和优化器, 并初始化了参数, 他想让你帮忙模拟神经网络的正向传播与反向传播过程, 将正确的值告诉他.
由于担心你的机器学习基础比小 M 更不好, 小 M 贴心地为你准备了一些基础概念, 以供参考:
神经元 (Neuron): 神经网络的基本计算单元,模拟生物神经元的工作方式, 负责接收输入, 进行加权计算并产生输出. 接受来自前一层神经元的输入 x1,x2,x3,...,xn 并与对应的权重 w1,w2,w3,...,wn 分别相乘后求和, 并与偏置 b 相加. 形式化地, 可以表示为:
z=∑i=1nwixi+b
正向传播 (Forward Propagation): 神经网络中进行预测的核心过程, 输入数据从输入层进入网络, 依次经过各隐藏层, 每一层的神经元通过加权求和 (输入与权重的线性结合) 并施加激活函数, 将结果传递到下一层, 最终在输出层生成预测值, 对于第 l 层, 形式化地表示为:
z(l)=σ(W(l)a(l−1)+b(l))
反向传播 (Backward Propagation): 神经网络中基于链式法则计算损失函数对输入的梯度 (偏导数) 的过程, 其核心是通过输出层向输入层逐层回传误差.
由于小 M 的编程能力很弱, 他设计的神经网络比较简单, 与真实的神经网络有很大差别, 小 Y 将这些特点总结给你:
小 M 的神经网络中, 对于任意神经元, 偏置 b 皆为 0, 且每个神经元恰好有两个输入, 每一层的激活函数皆为 ReLU 函数, ReLU 函数定义如下:
如果如果ReLU(x)={x如果x≥0,0如果x<0.
特别地,我们将 ReLU 函数在 x=0 处的导数值作为 0 来处理.
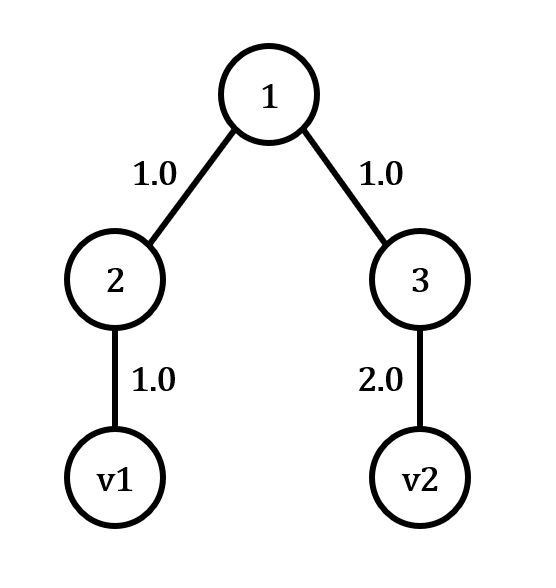
小 M 的神经网络固定有 N=2p−1 个节点, 结构固定是一个满二叉树. 输出层只有一个节点, 即为根节点, 根节点编号固定为 1. 对于编号为 k 的神经元, 与神经元输入端相连的节点编号固定为 2k 和 2k+1.
在针对某一个目的标签为 0 的任务的训练中, 小 W 将损失函数定义为输出本身, 即反向传播的目的便是计算输入层各分量对最终输出值的偏导数.
依据计算公式, 我们可以发现, 在这个任务中, 对于一个神经元, 其正向传播过程中, 输出 z 关于输入 x 和 w 的函数为:
z=ReLU(xinid1×Winid1+xinid2×winid2)
小 M 首先会告诉你一个神经网络的结构和权重, 在网络初始化完成后, 小 M 给你一个向量维度和输入端口数相同的输入向量 v.
在网络训练中, 会让你完成三种操作, 它们分别是:
修改输入: 对于输入向量的某一维度 vi 进行修改, 你需要给出神经网络新的输出结果 res, 结果保留一位小数.
反向传播: 求损失函数对于输入向量的第 i 维度 vi 的偏导数, 结果保留一位小数.
优化: 小 M 的肉眼优化器发挥作用, 对神经网络第 k 个神经元的所有输入对应的权重都乘以一个系数, 将其更新.
注意: 优化操作是对真实网络数据完成的更改, 对后续查询有后效性.